Определение сил взаимодействия в системе колесо — рельс на основании измерения напряжений в шейке рельса
Ю. С. Ромен, О. А. Суслов, А. А. Баляева
Акционерное общество «Научно-исследовательский институт железнодорожного транспорта» (АО «ВНИИЖТ»), Москва, 129626, Россия
Аннотация. Непосредственное измерение сил взаимодействия экипажа и пути практически невозможно. Их определение можно осуществлять, измеряя напряжения в рельсах, взаимозависимости которых с силами носят вероятностный характер. Корреляция показаний сил и напряжений для поезда в большинстве случаев находится в диапазоне 0,9 – 0,95. Практический метод определения сил взаимодействия по напряжениям в шейке рельса был предложен Шлумпфом. Получаемые результаты можно применять при проведении сертификационных испытаний. Точность метода цифровой обработки данных по напряжениям в трех точках шейки рельса существенно выше. Погрешность расчета сил не превосходит 4 %, что показывает целесообразность использования трехточечного метода при определении сил взаимодействия для установления условий обращения.
Ключевые слова: взаимодействие подвижного состава и пути; методы измерений сил взаимодействия; боковые силы; рамные силы; напряжения
Введение. При внедрении в эксплуатацию нового и модернизированного подвижного состава одной из основных проблем являются условия обеспечения как безопасности движения, так и прочности экипажа и пути, которые обуславливаются силами в системе колесо — рельс [1, 2]. В мировой практике исследований различают три компоненты силы взаимодействия: вертикальную, горизонтальную и продольную [1, 3]. Так как продольная составляющая не оказывает существенного влияния на устойчивость колеса на рельсе, при проведении динамических испытаний определяют одновременно (в одном сечении пути) величины только горизонтальных и вертикальных составляющих сил взаимодействия, которые имеют случайную величину, поскольку определяются множеством факторов.
Непосредственное измерение сил взаимодействия в контакте колесо – рельс практически невозможно. Однако, поскольку они обуславливают напряженное состояние как элементов конструкции пути, так и ходовых частей подвижного состава, их определение с известной степенью точности можно осуществлять, проводя соответствующие измерения напряжений как в пути, так и в элементах ходовых частей подвижного состава [3, 4, 5, 6].
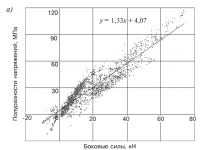
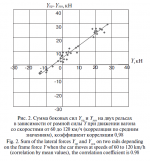
Напряжения и силы в системе колесо – рельс обуславливаются рядом параметров, часть из которых не являются строго фиксированными. Поэтому их взаимозависимости на подвижном составе и в пути носят не абсолютный, а вероятностный характер с достаточно высокими корреляционными связями. Корреляция показаний сил взаимодействия и напряжений в рельсе в большинстве случаев находится в диапазоне 0,9 – 0,95 и изменяется в зависимости от характера положения в колее соседних колесных пар при их набегании на рельс. На рис. 1 приведены величины полусумм и полуразностей кромочных напряжений подошвы в различных сечениях рельса, по которым можно оценивать величину вертикальных и боковых нагрузок [7, 8] под осями грузовых вагонов в сечениях пути при разных скоростях движения. На рис. 1, а видно, что в диапазоне величин боковых сил YБ до 20 кН выделяется группа точек, в которой коэффициент регрессии выше, чем для всей совокупности соотношения боковых сил и полуразности напряжений в кромках подошвы рельса. Эти точки зарегистрированы в основном при отсутствии набегания на рельс рассматриваемой колесной пары, когда на величину полуразности кромочных напряжений в данном сечении подошвы рельса оказывают ощутимое влияние силы воздействия соседних колес.
Силы, действующие от колеса на рельс. При определении параметров взаимодействия подвижного состава и пути наиболее целесообразно рассматривать систему координат рельса [1]. Ее элементы:
ось Х — касательная к оси пути, проходящая через центр рельса;
ось Y — горизонтальная ось, параллельная поперечной оси рельса;
ось Z — вертикальная ось рельса.
Разложение сил контактного взаимодействия в координатном пространстве XYZ характеризует разностороннее воздействие колеса на путь в рассматриваемом сечении.
Вертикальная сила P — сумма проекций на ось Z сил контактного взаимодействия. Ее действие распро-страняется на элементы промежуточных скреплений подрельсового основания, балластный и иные несущие слои вплоть до земляного полотна. Она определяет деградацию пути в части балластного слоя, вызывает изломы подкладок и шпал, износ резиновых прокладок, просадки и перекосы пути.
Продольная сила N — сумма проекций сил контактного взаимодействия на ось Х. Передается на элементы промежуточных рельсовых скреплений и через подрельсовое основание на балласт и нижележащие слои. Действие этой силы вызывает продольную деформацию пути, его угон и влияет на величину продольно-поперечного изгиба рельса.
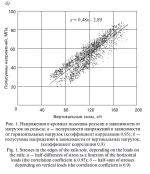
Боковая сила воздействия на рельс YБ — сумма проекций всех сил контактного взаимодействия на ось Y. Действует в первую очередь на удерживающие элементы скреплений и подрельсовое основание в поперечном направлении. Она является сдвигающей силой для элементов рельсошпальной решетки. Определяет прочность и износ элементов промежуточных рельсовых скреплений, вызывает изменение ширины колеи. Суммарное воздействие боковых сил Yпр и Yлев на правом и левом рельсах создает сдвигающую силу [9], действующую на всю рельсошпальную решетку и определяющую деградацию пути в плане. Если пренебречь инерционными процессами, то оно соответствует рамной силе, действующей на буксы колесной пары. Величина рамной силы создает поперечное воздействие на ходовые части и является одним из динамических параметров экипажа, результаты измерения которого характеризуют его устойчивость от схода и воздействие на путь. На рис. 2 приведены результаты измерений на экипаже рамных сил и суммы боковых на рельсах для грузового вагона в одном из сечений пути кривой радиусом 650 м [10]. Уровень корреляции этих параметров по их средним величинам составляет 0,98.
Следует отметить, что поскольку при измерениях боковые силы определяют по напряжениям в рельсе, а рамные — на подвижном составе, то вследствие неравноупругости пути под и над шпалами уровень их корреляции в междушпальных ящиках примерно на 10 % ниже, чем непосредственно над шпалой.
Основные методы измерений сил взаимодействия. При проведении испытаний подвижного состава основным является определение вертикальных и боковых сил, так как их величина и отношение определяют в первую очередь интенсивность расстройства пути и устойчивость колеса на рельсе.
До 60-х гг. прошлого века для определения напряженного состояния пути использовали в основном измерения кромочных напряжений в подошве рельса. Вследствие приведенных выше корреляционных зависимостей по их полусумме и полуразности оценивали величины вертикальных и боковых сил, действующих на рельс от подвижного состава.
Необходимо войти для просмотра
Необходимо войти для просмотра
Тензометрические датчики для измерения напряжений в динамике были изобретены в США в 1938 г. и предложены для измерений на железной дороге в 1944 г. [11]. В 1945 г. тензодатчики начали применяться на железных дорогах России. Вначале основным инструментом непосредственного измерения сил являлось определение максимальных деформаций под проходящим подвижным составом с последующим их умножением на соответствующие жесткости, которые определяли при статической калибровке.
В 1946 г. М. Ф. Вериго предложил для оценки динамического воздействия подвижного состава на путь ввести непрерывную регистрацию сил взаимодействия колеса и рельса, используя напряженное состояние диска колеса [12]. Этот метод в дальнейшем был реализован на локомотивах и грузовых вагонах [4, 5, 6, 13].
Необходимо войти для просмотра
В работе [14] приведены методы измерений сил взаимодействия, применяемые различными фирмами. С. П. Тимошенко указывал, что «для того чтобы получить вертикальную и боковую компоненты давления колеса на рельс в условиях эксплуатации, необходимо произвести измерение напряжения в трех волокнах рельса...» [11, с. 214].
Методика экспериментального определения вертикальных и боковых сил, действующих на рельс, по измерению напряжений (деформаций) в трех точках его сечения (по наружной стороне головки и по двум кромкам подошвы) была разработана О. П. Ершковым под руководством Е. М. Бромберга [15, 16]. В соответствии с применявшейся методикой оценки взаимодействия по кромочным напряжениям параметры силового воздействия определяли по формулам:
Необходимо войти для просмотра
где Необходимо войти для просмотра — показания датчиков в наружной, внутренней кромках подошвы и на наружной стороне головки рельса; h — превышение плоскости действия боковой силы над центром изгиба сечения, положение которого может не совпадать с положением нейтральной оси сечения; e — эксцентриситет приложения вертикальной нагрузки относительно продольной оси рельса; A1, A2, B1, B2, B3 — расчетные коэффициенты, определяемые по положению мест наклейки датчиков, плоскости приложения боковой силы и размеров элементов сечения рельса.
При отсутствии электронной портативной вычислительной техники трехточечный метод О. П. Ершкова был достаточно трудоемким, так как требовал проведения большого количества расчетов. Поэтому для проведения серийных испытаний он был заменен методом Шлумпфа [17, 18], разработанным для определения силового воздействия на рельс по измерениям деформаций шейки рельса. Метод заключается в определении разности моментов в двух сечениях шейки рельса, в которых моменты сопротивления изгиба одинаковы. Имеем
Необходимо войти для просмотра
где hа и hb — плечо приложения боковой силы относительно каждого из поперечных сечений (a и b). Если величины моментов сопротивления и площади горизонтальных сечений шейки в местах наклейки тензодатчиков равны, то при равенстве масштабных коэффициентов по разности моментов изгиба определяют величину боковой силы
Необходимо войти для просмотра
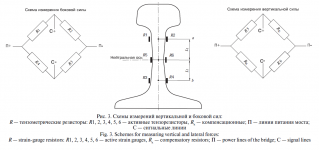
При отсутствии в 50-х гг. мощной цифровой вычислительной техники четыре тензорезистора (R1, R2, R3, R4) включали в плечи одного моста Уитстона, а для определения вертикальной нагрузки использовали еще одну пару датчиков (R5,R6) и мост (рис. 3). Опыты А. К. Шафрановского [13] показали, что в случае правильно выбранных сечений для мест наклейки и одинаковых коэффициентах передачи датчиков эксцентриситет приложения нагрузки практически не влияет на результаты измерений. Принципиальной неточностью метода Шлумпфа являлось допущение, что слагаемое Pe в формуле для определения момента во всех сечениях одинаково [19]. В действительности этим допущением можно пользоваться в том случае, когда расстояние по высоте между сечениями достаточно мало [20] по сравнению с расстоянием до точки приложения силы.
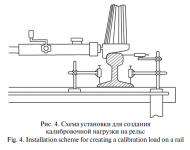
Поскольку при определении условий обращения рассматривают максимальные величины боковых сил взаимодействия, которые возникают при набегании гребнем колеса на головку рельса, для проведения калибровок на домкратной тарировочной установке применялся специальный адаптер с поверхностью, аналогичной профилю колеса (рис. 4) [3]. Это позволяло в процессе калибровок имитировать силовые процессы в контакте при набегании колеса на рельс, что уменьшало погрешности, возникающие в системе вследствие неточности определения мест наклейки датчиков и разности размеров шейки рельса в измеряемых сечениях. Следует отметить, что хотя указанные погрешности не позволяют полностью нивелировать влияние момента Pe в мостовых схемах при вычитаниях в соответствии с формулами (4) и (5), их влияние не приводит к существенным неточностям при оценке и сравнении максимальных величин сил взаимодействия различных экипажей. Обуславливается это тем, что максимальные величины сил взаимодействия имеют место при набегании колеса на рельс в точках контакта, которые определяются размерами головки рельса, и поэтому величина эксцентриситета e в данном сечении примерно одинакова для всех экипажей.
Необходимо войти для просмотра
Применение вычислительной техники при определении сил взаимодействия по измерениям напряжений в шейке рельса. Внедрение в процессы обработки данных средств цифровой вычислительной техники позволяет избегать погрешностей метода Шлумпфа, возникающих вследствие неточности определения мест расположения тензометрических схем и различия в масштабных коэффициентах регистрируемых сигналов.
В частности, в методике «РЖД-2016» [21] реализуется замена электрической аппаратной обработки аналоговых сигналов по Шлумпфу математической. Определение напряжений в каждой из четырех точек наклейки проводится в этом случае отдельной мостовой схемой. Это вдвое увеличивает число используемых тензодатчиков (до 16) и каналов измерения (до 4). Однако, поскольку в основе данного экспериментально-расчетного метода лежит использование матриц влияния, в этом случае для определения действующих на рельс сил по напряжениям в местах наклейки первичных тензометрических преобразователей (тензорезисторов) не требуется точной наклейки тензорезисторов.
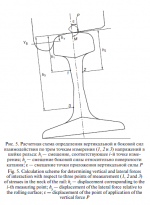
При использовании, согласно С. П. Тимошенко, измерения напряжений не в четырех, а в трех точках рельса [11] количество аппаратуры существенно уменьшается. В предлагаемом методе вместо 8 тензодатчиков, объединяемых в два моста, которые используются при определении боковой и вертикальной силы по методике Шлумпфа, напряжения измеряют тремя полумостовыми схемами на шейке рельса с наклейкой 6 тензодатчиков (рис. 5).
Если датчики 1 и 3 расположены с внутренней стороны рельса, а датчик 2 — с наружной, то выражения для определения напряжений в трех i-х сечениях шейки рельса имеют вид:
Необходимо войти для просмотра
где σi — напряжения, в сечениях шейки рельса (i — номер точки измерения); P — вертикальная сила, действующая от колеса на рельс на поверхности катания головки рельса; Y — боковая сила, действующая от колеса на рельс на головку рельса; M = Pe — момент вертикальной силы при поперечном смещении точки контакта на головке рельса; a, b, c — элементы матрицы напряжений, являющиеся соответствующими коэффициентами влияния в выражениях для напряжений при нагрузках на рельс
Необходимо войти для просмотра
где Fi — площадь соответствующего сечения шейки рельса; Wi — момент сопротивления в данном сечении; hi — расстояние от поверхности катания на головке рельса до центра измерительного тензорезистора в i-м сечении шейки; hy — расстояние от поверхности катания рельса до точки приложения боковой силы.
Необходимо войти для просмотра
Необходимо войти для просмотра
Совокупность измеряемых напряжений σi, описываемых уравнениями (6), представляет систему трех уравнений с тремя неизвестными силовыми параметрами. Определение боковой силы производится не по разности моментов Ma − Mb, вызывающих соответствующие напряжения, как это реализовано в методе Шлумпфа (5), а в результате решения системы уравнений по данным замеров в местах наклейки датчиков и коэффициентов передачи датчиков. Повышение количества усилительных каналов увеличивает используемое оборудование и трудоемкость работ. Однако при математической обработке измерений уменьшается погрешность определения сил взаимодействия, так как жесткостные параметры рельса и значения коэффициентов передачи датчиков входят в величины коэффициентов влияния (7), которые
определяются при калибровке.
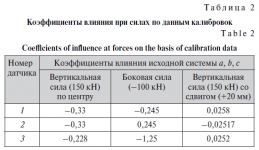
Элементы матрицы влияния ai, bi, ci определяют в результате калибровочных нагружений рельса по формулам (7) с учетом соответствующих знаков в уравнениях (6) и значений коэффициентов передачи Kip, Kiy, KiM.
В результате тарировочных нагружений получают зависимости напряжений σi от действующих сил для вычисления коэффициентов влияния (7), которые являются неизвестными в системе (6), при известных калибровочных силах и обуславливаемых ими напряжениях. Эти коэффициенты определяются при трехкратном калибровочном приложении различных систем нагрузок и дают возможность реализации обратной операции — определение сил по известным напряжениям, когда в уравнениях (6) при известных коэффициентах (7) в качестве неизвестных выступают силы.
Рассмотрим методику калибровки.
1. При отсутствии боковой силы нагружаем рельс вертикальной силой P известной величины по центру головки (Y =0, e=0). В том случае ai = σi / P.
2. Нагружаем рельс вертикальной силой P при заданном поперечном смещении точки ее приложения (Y =0, M = Pe). По результатам измерения напряжений получаем для каждого из уравнений системы (6) величины
Необходимо войти для просмотра
3. Для определения величин коэффициентов влияния боковых сил bi при расчетной реализации рассматриваемой обработки данных методом конечных элементов можно использовать калибровку приложением заданной боковой силы Y при P = 0. В этом случае
Необходимо войти для просмотра
Однако в эксперименте, а тем более в полевых условиях организовать подобное нагружение достаточно сложно. К тому же в реальности приложение боковых сил сопровождается вертикальным воздействием колесной нагрузки. Потому калибровку боковой силой производят с вертикальным пригрузоv известной вертикальной центральной нагрузкой, и расчет ведется по формуле
Необходимо войти для просмотра
Решение системы трех линейных уравнений для определения величины сил взаимодействия в зависимости от напряженного состояния рельса в рассматриваемом его сечении имеет вид:
Необходимо войти для просмотра
где S1, 2, 3 — показания соответствующего датчика под действующей в рассматриваемом сечении рельса системой нагрузок.
Коэффициенты матрицы (8) AP1, BP2, CP3, AY1, BY2, CY3, AM1, BM2 и CM3 определяются решением уравнений (6) либо по формулам Крамера, что для системы трех линейных уравнений не представляет трудностей, либо как элементы псевдообратной матрицы с использованием соответствующей системы программ [22].
Необходимо войти для просмотра
Верификация рассматриваемого метода измерений сил взаимодействия. Для проверки рассматриваемого метода была разработана конечно-элементная модель, позволяющая теоретически получать напряжения в точках измерения для сопоставления с результатами эксперимента на стенде (рис. 6). Экспериментальная модель представляет отрезок рельса длиной 60 см, закрепленный с двух сторон в зоне опирания рельса на подкладки. На основе разработанной модели были выполнены вариантные расчеты нагружения рельса различными сочетаниями вертикальной и боковой сил.
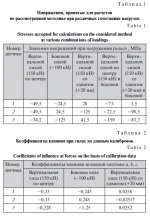
При верификации метода для определения влияния положения точки контакта на головке рельса осуществляли центральное нагружение вертикальной силой и ее смещение вправо и влево относительно продольной оси. В процессе нагружения проводилась фиксация напряжений в точках шейки рельса в соответствии с расчетной схемой. Расхождение результатов измеренных напряжений и их расчетных значений, полученных при конечноэлементном моделировании, лежит в пределах 8 %.
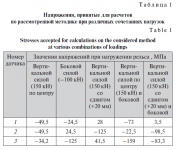
На основе полученных данных были приняты величины напряжений для верификации рассматриваемого метода определения сил взаимодействия по измеренным напряжениям.
При решении уравнений (8) по методу Крамера глаdный определитель системы D вычисляется по формуле
Необходимо войти для просмотра
Раскрывая дополнительные определители системы, получаем выражения для расчета сил взаимодействия по данным показаний датчиков S1, S2, S3:
Необходимо войти для просмотра
Проведенная серия экспериментов показала, что различие опытных и расчетных данных не превосходит 4 %. Полученные результаты позволяют сделать вывод о целесообразности ввода в пробную эксплуатацию предложенной трехточечной схемы измерения сил для сравнительной оценки, в том числе с методом ГОСТ Р 55050 – 2012 (метод Шлумпфа) и методом «РЖД-2016».
Необходимо войти для просмотра
Выводы. 1. Метод измерения боковой силы с электрической обработкой сигнала (метод Шлумпфа) при недостаточной точности наклейки датчиков обладает значительной зависимостью показаний измерений от точки
приложения вертикальной силы относительно оси рельса, уступая по точности цифровой обработке экспериментальных данных. Однако, поскольку при установлении условий обращения подвижного состава рассматриваются максимальные значения сил взаимодействия, реализуемые в основном при набегании колеса на рельс, когда смещение вертикальной нагрузки определяется параметрами головки рельса и изменяется незначительно, получаемые результаты можно применять при проведении сертификационных испытаний.
2. Метод цифровой обработки данных при определении сил взаимодействия по напряжениям в трех точках шейки рельса требует для своей реализации три тензометрических моста вместо двух, однако точность его результатов существенно выше, так как зависит только от погрешностей предварительной калибровки сечений.
3. Полученные результаты показывают целесообразность использования предлагаемого трехточечного метода при определении взаимодействия подвижного состава и пути для установления условий обращения.
Ю. С. Ромен, О. А. Суслов, А. А. Баляева
Акционерное общество «Научно-исследовательский институт железнодорожного транспорта» (АО «ВНИИЖТ»), Москва, 129626, Россия
Аннотация. Непосредственное измерение сил взаимодействия экипажа и пути практически невозможно. Их определение можно осуществлять, измеряя напряжения в рельсах, взаимозависимости которых с силами носят вероятностный характер. Корреляция показаний сил и напряжений для поезда в большинстве случаев находится в диапазоне 0,9 – 0,95. Практический метод определения сил взаимодействия по напряжениям в шейке рельса был предложен Шлумпфом. Получаемые результаты можно применять при проведении сертификационных испытаний. Точность метода цифровой обработки данных по напряжениям в трех точках шейки рельса существенно выше. Погрешность расчета сил не превосходит 4 %, что показывает целесообразность использования трехточечного метода при определении сил взаимодействия для установления условий обращения.
Ключевые слова: взаимодействие подвижного состава и пути; методы измерений сил взаимодействия; боковые силы; рамные силы; напряжения
Введение. При внедрении в эксплуатацию нового и модернизированного подвижного состава одной из основных проблем являются условия обеспечения как безопасности движения, так и прочности экипажа и пути, которые обуславливаются силами в системе колесо — рельс [1, 2]. В мировой практике исследований различают три компоненты силы взаимодействия: вертикальную, горизонтальную и продольную [1, 3]. Так как продольная составляющая не оказывает существенного влияния на устойчивость колеса на рельсе, при проведении динамических испытаний определяют одновременно (в одном сечении пути) величины только горизонтальных и вертикальных составляющих сил взаимодействия, которые имеют случайную величину, поскольку определяются множеством факторов.
Непосредственное измерение сил взаимодействия в контакте колесо – рельс практически невозможно. Однако, поскольку они обуславливают напряженное состояние как элементов конструкции пути, так и ходовых частей подвижного состава, их определение с известной степенью точности можно осуществлять, проводя соответствующие измерения напряжений как в пути, так и в элементах ходовых частей подвижного состава [3, 4, 5, 6].
Напряжения и силы в системе колесо – рельс обуславливаются рядом параметров, часть из которых не являются строго фиксированными. Поэтому их взаимозависимости на подвижном составе и в пути носят не абсолютный, а вероятностный характер с достаточно высокими корреляционными связями. Корреляция показаний сил взаимодействия и напряжений в рельсе в большинстве случаев находится в диапазоне 0,9 – 0,95 и изменяется в зависимости от характера положения в колее соседних колесных пар при их набегании на рельс. На рис. 1 приведены величины полусумм и полуразностей кромочных напряжений подошвы в различных сечениях рельса, по которым можно оценивать величину вертикальных и боковых нагрузок [7, 8] под осями грузовых вагонов в сечениях пути при разных скоростях движения. На рис. 1, а видно, что в диапазоне величин боковых сил YБ до 20 кН выделяется группа точек, в которой коэффициент регрессии выше, чем для всей совокупности соотношения боковых сил и полуразности напряжений в кромках подошвы рельса. Эти точки зарегистрированы в основном при отсутствии набегания на рельс рассматриваемой колесной пары, когда на величину полуразности кромочных напряжений в данном сечении подошвы рельса оказывают ощутимое влияние силы воздействия соседних колес.
Силы, действующие от колеса на рельс. При определении параметров взаимодействия подвижного состава и пути наиболее целесообразно рассматривать систему координат рельса [1]. Ее элементы:
ось Х — касательная к оси пути, проходящая через центр рельса;
ось Y — горизонтальная ось, параллельная поперечной оси рельса;
ось Z — вертикальная ось рельса.
Разложение сил контактного взаимодействия в координатном пространстве XYZ характеризует разностороннее воздействие колеса на путь в рассматриваемом сечении.
Вертикальная сила P — сумма проекций на ось Z сил контактного взаимодействия. Ее действие распро-страняется на элементы промежуточных скреплений подрельсового основания, балластный и иные несущие слои вплоть до земляного полотна. Она определяет деградацию пути в части балластного слоя, вызывает изломы подкладок и шпал, износ резиновых прокладок, просадки и перекосы пути.
Продольная сила N — сумма проекций сил контактного взаимодействия на ось Х. Передается на элементы промежуточных рельсовых скреплений и через подрельсовое основание на балласт и нижележащие слои. Действие этой силы вызывает продольную деформацию пути, его угон и влияет на величину продольно-поперечного изгиба рельса.
Боковая сила воздействия на рельс YБ — сумма проекций всех сил контактного взаимодействия на ось Y. Действует в первую очередь на удерживающие элементы скреплений и подрельсовое основание в поперечном направлении. Она является сдвигающей силой для элементов рельсошпальной решетки. Определяет прочность и износ элементов промежуточных рельсовых скреплений, вызывает изменение ширины колеи. Суммарное воздействие боковых сил Yпр и Yлев на правом и левом рельсах создает сдвигающую силу [9], действующую на всю рельсошпальную решетку и определяющую деградацию пути в плане. Если пренебречь инерционными процессами, то оно соответствует рамной силе, действующей на буксы колесной пары. Величина рамной силы создает поперечное воздействие на ходовые части и является одним из динамических параметров экипажа, результаты измерения которого характеризуют его устойчивость от схода и воздействие на путь. На рис. 2 приведены результаты измерений на экипаже рамных сил и суммы боковых на рельсах для грузового вагона в одном из сечений пути кривой радиусом 650 м [10]. Уровень корреляции этих параметров по их средним величинам составляет 0,98.
Следует отметить, что поскольку при измерениях боковые силы определяют по напряжениям в рельсе, а рамные — на подвижном составе, то вследствие неравноупругости пути под и над шпалами уровень их корреляции в междушпальных ящиках примерно на 10 % ниже, чем непосредственно над шпалой.
Основные методы измерений сил взаимодействия. При проведении испытаний подвижного состава основным является определение вертикальных и боковых сил, так как их величина и отношение определяют в первую очередь интенсивность расстройства пути и устойчивость колеса на рельсе.
До 60-х гг. прошлого века для определения напряженного состояния пути использовали в основном измерения кромочных напряжений в подошве рельса. Вследствие приведенных выше корреляционных зависимостей по их полусумме и полуразности оценивали величины вертикальных и боковых сил, действующих на рельс от подвижного состава.
Необходимо войти для просмотра
Необходимо войти для просмотра
Тензометрические датчики для измерения напряжений в динамике были изобретены в США в 1938 г. и предложены для измерений на железной дороге в 1944 г. [11]. В 1945 г. тензодатчики начали применяться на железных дорогах России. Вначале основным инструментом непосредственного измерения сил являлось определение максимальных деформаций под проходящим подвижным составом с последующим их умножением на соответствующие жесткости, которые определяли при статической калибровке.
В 1946 г. М. Ф. Вериго предложил для оценки динамического воздействия подвижного состава на путь ввести непрерывную регистрацию сил взаимодействия колеса и рельса, используя напряженное состояние диска колеса [12]. Этот метод в дальнейшем был реализован на локомотивах и грузовых вагонах [4, 5, 6, 13].
Необходимо войти для просмотра
В работе [14] приведены методы измерений сил взаимодействия, применяемые различными фирмами. С. П. Тимошенко указывал, что «для того чтобы получить вертикальную и боковую компоненты давления колеса на рельс в условиях эксплуатации, необходимо произвести измерение напряжения в трех волокнах рельса...» [11, с. 214].
Методика экспериментального определения вертикальных и боковых сил, действующих на рельс, по измерению напряжений (деформаций) в трех точках его сечения (по наружной стороне головки и по двум кромкам подошвы) была разработана О. П. Ершковым под руководством Е. М. Бромберга [15, 16]. В соответствии с применявшейся методикой оценки взаимодействия по кромочным напряжениям параметры силового воздействия определяли по формулам:
Необходимо войти для просмотра
где Необходимо войти для просмотра — показания датчиков в наружной, внутренней кромках подошвы и на наружной стороне головки рельса; h — превышение плоскости действия боковой силы над центром изгиба сечения, положение которого может не совпадать с положением нейтральной оси сечения; e — эксцентриситет приложения вертикальной нагрузки относительно продольной оси рельса; A1, A2, B1, B2, B3 — расчетные коэффициенты, определяемые по положению мест наклейки датчиков, плоскости приложения боковой силы и размеров элементов сечения рельса.
При отсутствии электронной портативной вычислительной техники трехточечный метод О. П. Ершкова был достаточно трудоемким, так как требовал проведения большого количества расчетов. Поэтому для проведения серийных испытаний он был заменен методом Шлумпфа [17, 18], разработанным для определения силового воздействия на рельс по измерениям деформаций шейки рельса. Метод заключается в определении разности моментов в двух сечениях шейки рельса, в которых моменты сопротивления изгиба одинаковы. Имеем
Необходимо войти для просмотра
где hа и hb — плечо приложения боковой силы относительно каждого из поперечных сечений (a и b). Если величины моментов сопротивления и площади горизонтальных сечений шейки в местах наклейки тензодатчиков равны, то при равенстве масштабных коэффициентов по разности моментов изгиба определяют величину боковой силы
Необходимо войти для просмотра
При отсутствии в 50-х гг. мощной цифровой вычислительной техники четыре тензорезистора (R1, R2, R3, R4) включали в плечи одного моста Уитстона, а для определения вертикальной нагрузки использовали еще одну пару датчиков (R5,R6) и мост (рис. 3). Опыты А. К. Шафрановского [13] показали, что в случае правильно выбранных сечений для мест наклейки и одинаковых коэффициентах передачи датчиков эксцентриситет приложения нагрузки практически не влияет на результаты измерений. Принципиальной неточностью метода Шлумпфа являлось допущение, что слагаемое Pe в формуле для определения момента во всех сечениях одинаково [19]. В действительности этим допущением можно пользоваться в том случае, когда расстояние по высоте между сечениями достаточно мало [20] по сравнению с расстоянием до точки приложения силы.
Поскольку при определении условий обращения рассматривают максимальные величины боковых сил взаимодействия, которые возникают при набегании гребнем колеса на головку рельса, для проведения калибровок на домкратной тарировочной установке применялся специальный адаптер с поверхностью, аналогичной профилю колеса (рис. 4) [3]. Это позволяло в процессе калибровок имитировать силовые процессы в контакте при набегании колеса на рельс, что уменьшало погрешности, возникающие в системе вследствие неточности определения мест наклейки датчиков и разности размеров шейки рельса в измеряемых сечениях. Следует отметить, что хотя указанные погрешности не позволяют полностью нивелировать влияние момента Pe в мостовых схемах при вычитаниях в соответствии с формулами (4) и (5), их влияние не приводит к существенным неточностям при оценке и сравнении максимальных величин сил взаимодействия различных экипажей. Обуславливается это тем, что максимальные величины сил взаимодействия имеют место при набегании колеса на рельс в точках контакта, которые определяются размерами головки рельса, и поэтому величина эксцентриситета e в данном сечении примерно одинакова для всех экипажей.
Необходимо войти для просмотра
Применение вычислительной техники при определении сил взаимодействия по измерениям напряжений в шейке рельса. Внедрение в процессы обработки данных средств цифровой вычислительной техники позволяет избегать погрешностей метода Шлумпфа, возникающих вследствие неточности определения мест расположения тензометрических схем и различия в масштабных коэффициентах регистрируемых сигналов.
В частности, в методике «РЖД-2016» [21] реализуется замена электрической аппаратной обработки аналоговых сигналов по Шлумпфу математической. Определение напряжений в каждой из четырех точек наклейки проводится в этом случае отдельной мостовой схемой. Это вдвое увеличивает число используемых тензодатчиков (до 16) и каналов измерения (до 4). Однако, поскольку в основе данного экспериментально-расчетного метода лежит использование матриц влияния, в этом случае для определения действующих на рельс сил по напряжениям в местах наклейки первичных тензометрических преобразователей (тензорезисторов) не требуется точной наклейки тензорезисторов.
При использовании, согласно С. П. Тимошенко, измерения напряжений не в четырех, а в трех точках рельса [11] количество аппаратуры существенно уменьшается. В предлагаемом методе вместо 8 тензодатчиков, объединяемых в два моста, которые используются при определении боковой и вертикальной силы по методике Шлумпфа, напряжения измеряют тремя полумостовыми схемами на шейке рельса с наклейкой 6 тензодатчиков (рис. 5).
Если датчики 1 и 3 расположены с внутренней стороны рельса, а датчик 2 — с наружной, то выражения для определения напряжений в трех i-х сечениях шейки рельса имеют вид:
Необходимо войти для просмотра
где σi — напряжения, в сечениях шейки рельса (i — номер точки измерения); P — вертикальная сила, действующая от колеса на рельс на поверхности катания головки рельса; Y — боковая сила, действующая от колеса на рельс на головку рельса; M = Pe — момент вертикальной силы при поперечном смещении точки контакта на головке рельса; a, b, c — элементы матрицы напряжений, являющиеся соответствующими коэффициентами влияния в выражениях для напряжений при нагрузках на рельс
Необходимо войти для просмотра
где Fi — площадь соответствующего сечения шейки рельса; Wi — момент сопротивления в данном сечении; hi — расстояние от поверхности катания на головке рельса до центра измерительного тензорезистора в i-м сечении шейки; hy — расстояние от поверхности катания рельса до точки приложения боковой силы.
Необходимо войти для просмотра
Необходимо войти для просмотра
Совокупность измеряемых напряжений σi, описываемых уравнениями (6), представляет систему трех уравнений с тремя неизвестными силовыми параметрами. Определение боковой силы производится не по разности моментов Ma − Mb, вызывающих соответствующие напряжения, как это реализовано в методе Шлумпфа (5), а в результате решения системы уравнений по данным замеров в местах наклейки датчиков и коэффициентов передачи датчиков. Повышение количества усилительных каналов увеличивает используемое оборудование и трудоемкость работ. Однако при математической обработке измерений уменьшается погрешность определения сил взаимодействия, так как жесткостные параметры рельса и значения коэффициентов передачи датчиков входят в величины коэффициентов влияния (7), которые
определяются при калибровке.
Элементы матрицы влияния ai, bi, ci определяют в результате калибровочных нагружений рельса по формулам (7) с учетом соответствующих знаков в уравнениях (6) и значений коэффициентов передачи Kip, Kiy, KiM.
В результате тарировочных нагружений получают зависимости напряжений σi от действующих сил для вычисления коэффициентов влияния (7), которые являются неизвестными в системе (6), при известных калибровочных силах и обуславливаемых ими напряжениях. Эти коэффициенты определяются при трехкратном калибровочном приложении различных систем нагрузок и дают возможность реализации обратной операции — определение сил по известным напряжениям, когда в уравнениях (6) при известных коэффициентах (7) в качестве неизвестных выступают силы.
Рассмотрим методику калибровки.
1. При отсутствии боковой силы нагружаем рельс вертикальной силой P известной величины по центру головки (Y =0, e=0). В том случае ai = σi / P.
2. Нагружаем рельс вертикальной силой P при заданном поперечном смещении точки ее приложения (Y =0, M = Pe). По результатам измерения напряжений получаем для каждого из уравнений системы (6) величины
Необходимо войти для просмотра
3. Для определения величин коэффициентов влияния боковых сил bi при расчетной реализации рассматриваемой обработки данных методом конечных элементов можно использовать калибровку приложением заданной боковой силы Y при P = 0. В этом случае
Необходимо войти для просмотра
Однако в эксперименте, а тем более в полевых условиях организовать подобное нагружение достаточно сложно. К тому же в реальности приложение боковых сил сопровождается вертикальным воздействием колесной нагрузки. Потому калибровку боковой силой производят с вертикальным пригрузоv известной вертикальной центральной нагрузкой, и расчет ведется по формуле
Необходимо войти для просмотра
Решение системы трех линейных уравнений для определения величины сил взаимодействия в зависимости от напряженного состояния рельса в рассматриваемом его сечении имеет вид:
Необходимо войти для просмотра
где S1, 2, 3 — показания соответствующего датчика под действующей в рассматриваемом сечении рельса системой нагрузок.
Коэффициенты матрицы (8) AP1, BP2, CP3, AY1, BY2, CY3, AM1, BM2 и CM3 определяются решением уравнений (6) либо по формулам Крамера, что для системы трех линейных уравнений не представляет трудностей, либо как элементы псевдообратной матрицы с использованием соответствующей системы программ [22].
Необходимо войти для просмотра
Верификация рассматриваемого метода измерений сил взаимодействия. Для проверки рассматриваемого метода была разработана конечно-элементная модель, позволяющая теоретически получать напряжения в точках измерения для сопоставления с результатами эксперимента на стенде (рис. 6). Экспериментальная модель представляет отрезок рельса длиной 60 см, закрепленный с двух сторон в зоне опирания рельса на подкладки. На основе разработанной модели были выполнены вариантные расчеты нагружения рельса различными сочетаниями вертикальной и боковой сил.
При верификации метода для определения влияния положения точки контакта на головке рельса осуществляли центральное нагружение вертикальной силой и ее смещение вправо и влево относительно продольной оси. В процессе нагружения проводилась фиксация напряжений в точках шейки рельса в соответствии с расчетной схемой. Расхождение результатов измеренных напряжений и их расчетных значений, полученных при конечноэлементном моделировании, лежит в пределах 8 %.
На основе полученных данных были приняты величины напряжений для верификации рассматриваемого метода определения сил взаимодействия по измеренным напряжениям.
При решении уравнений (8) по методу Крамера глаdный определитель системы D вычисляется по формуле
Необходимо войти для просмотра
Раскрывая дополнительные определители системы, получаем выражения для расчета сил взаимодействия по данным показаний датчиков S1, S2, S3:
Необходимо войти для просмотра
Проведенная серия экспериментов показала, что различие опытных и расчетных данных не превосходит 4 %. Полученные результаты позволяют сделать вывод о целесообразности ввода в пробную эксплуатацию предложенной трехточечной схемы измерения сил для сравнительной оценки, в том числе с методом ГОСТ Р 55050 – 2012 (метод Шлумпфа) и методом «РЖД-2016».
Необходимо войти для просмотра
Выводы. 1. Метод измерения боковой силы с электрической обработкой сигнала (метод Шлумпфа) при недостаточной точности наклейки датчиков обладает значительной зависимостью показаний измерений от точки
приложения вертикальной силы относительно оси рельса, уступая по точности цифровой обработке экспериментальных данных. Однако, поскольку при установлении условий обращения подвижного состава рассматриваются максимальные значения сил взаимодействия, реализуемые в основном при набегании колеса на рельс, когда смещение вертикальной нагрузки определяется параметрами головки рельса и изменяется незначительно, получаемые результаты можно применять при проведении сертификационных испытаний.
2. Метод цифровой обработки данных при определении сил взаимодействия по напряжениям в трех точках шейки рельса требует для своей реализации три тензометрических моста вместо двух, однако точность его результатов существенно выше, так как зависит только от погрешностей предварительной калибровки сечений.
3. Полученные результаты показывают целесообразность использования предлагаемого трехточечного метода при определении взаимодействия подвижного состава и пути для установления условий обращения.
Вложения
-
 1.png21.2 KB · Просмотры: 80
1.png21.2 KB · Просмотры: 80 -
 10.png35.8 KB · Просмотры: 80
10.png35.8 KB · Просмотры: 80 -
 9.png22.8 KB · Просмотры: 80
9.png22.8 KB · Просмотры: 80 -
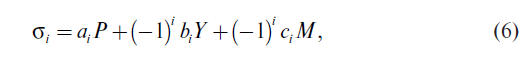 8.png4 KB · Просмотры: 80
8.png4 KB · Просмотры: 80 -
 7.png54.6 KB · Просмотры: 79
7.png54.6 KB · Просмотры: 79 -
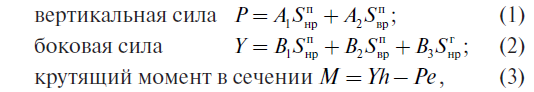 6.png15.1 KB · Просмотры: 81
6.png15.1 KB · Просмотры: 81 -
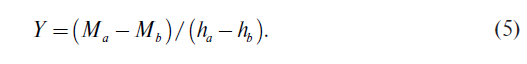 5.png4 KB · Просмотры: 81
5.png4 KB · Просмотры: 81 -
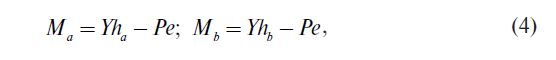 4.png4 KB · Просмотры: 79
4.png4 KB · Просмотры: 79 -
 3.png43.3 KB · Просмотры: 82
3.png43.3 KB · Просмотры: 82 -
 2.png61.3 KB · Просмотры: 80
2.png61.3 KB · Просмотры: 80 -
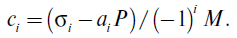 20.png2.8 KB · Просмотры: 76
20.png2.8 KB · Просмотры: 76 -
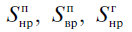 19.png1.9 KB · Просмотры: 80
19.png1.9 KB · Просмотры: 80 -
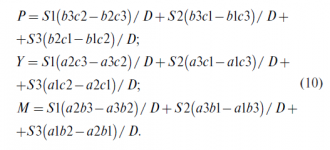 18.png24.1 KB · Просмотры: 75
18.png24.1 KB · Просмотры: 75 -
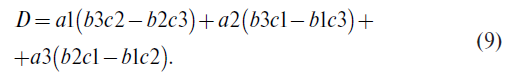 17.png6.6 KB · Просмотры: 74
17.png6.6 KB · Просмотры: 74 -
 16.png34.2 KB · Просмотры: 3
16.png34.2 KB · Просмотры: 3 -
 15.png51.7 KB · Просмотры: 3
15.png51.7 KB · Просмотры: 3 -
 14.png113.1 KB · Просмотры: 76
14.png113.1 KB · Просмотры: 76 -
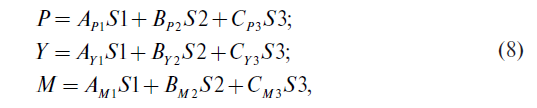 13.png10.7 KB · Просмотры: 75
13.png10.7 KB · Просмотры: 75 -
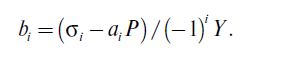 12.png2.9 KB · Просмотры: 76
12.png2.9 KB · Просмотры: 76 -
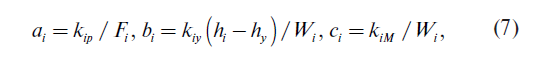 11.png5.3 KB · Просмотры: 79
11.png5.3 KB · Просмотры: 79 -
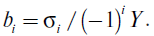 21.png1.9 KB · Просмотры: 76
21.png1.9 KB · Просмотры: 76 -
 22.png47.8 KB · Просмотры: 76
22.png47.8 KB · Просмотры: 76